교재링크(광고 아님): freelec.co.kr/book/인공지능을-위한-수학/
※ 교재의 내용에서 좀 더 보강이 필요하여 잔차(residual)와 최소절대편차(least absolute deviation) 등을 추가함.
잔차(residual)
관측값(observed value)과 예측값(predicted value)의 차이를 나타내는 값. 관측값과 예측값은 선형회귀에서는 y에 해당하는 값이며, 전자는 데이터, 후자는 모델에 의해 도출된 값이다. 아래 그래프를 보면 이해가 쉬울 것이다.
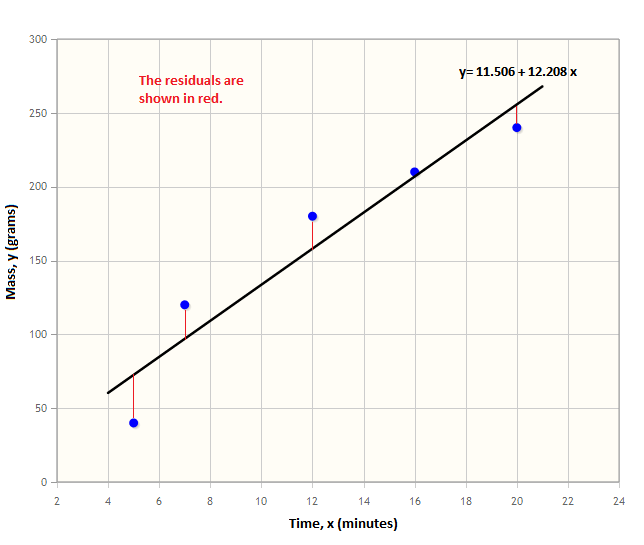
위 그래프에서 직선은 모델이고, 파란색 점은 관측값이다. 빨간선이 바로 잔차(residual)이며, 최소제곱법은 이 잔차를 이용한 방법론(methodology)이다.
잔차는 아래의 수식으로 표현한다.
$$ r_i = y_i - \hat{y_i} $$ $$ 잔차 = 관측값 - 예측값 $$
여기서 예측값에 대한 모델이 예제 그래프와 같이 1차식(직선)이라면 아래처럼 표현할 수도 있다.
$$ \hat{y_i} = f(x) = a + bx_i $$ $$ r_i = y_i - f(x) = y_i - (a + bx_i) $$
결론적으로 마지막 수식이 아래에 기술할 최소제곱법에서 쓰이게 된다.
최소제곱법(least squares method)
앞 절에서 알아본 선형회귀를 해결하기 위한 가장 기본적인 방법이 바로 이 최소제곱법이다. 위에서 설명한 잔차(residual)들의 합을 최소화하기 위해 고안된 방법이다. 그런데, 교재의 수식5.4.1을 보면 아래와 같이 나오는데,
$$ D = \sum_{l=1}^{4}{|y_l - (w_0 + w_1x_l)|} $$
이렇게 잔차에 절대값을 씌운 것을 먼저 설명하고 있다. 이 수식은 아래에 기술할 최소절대편차를 나타낸 것인데, 이는 현대에도 실제로 쓰이는 방법이며 (연관성은 크지만)최소제곱법을 도출하기 위한 일련의 과정처럼 설명하기에는 근거가 부족해 보인다. 최소한 내가 조사한 바에 의하면 그러한데, 차후에 공부를 더 해보면 왜 이렇게 저술했는지 알 수 있겠지.
어쨌든, 최소제곱법으로 나타낸 수식은 아래와 같다. (잔차식을 이용)
$$ S = \sum_{i=1}^{n}{{r_i}^2} $$
이를 좀 더 선형회귀에 어울리게 표현하면,
$$ \hat{y_i} = f(x, w) = w_0 + w_1x_i $$
$$ S = \sum_{i=1}^{n}{{[y_i - f(x, w)]}^2} $$
$$ S = \sum_{i=1}^{n}{{(y_i - w_0 - w_1x_i)}^2} $$
최소절대편차(least absolute deviation)
교재의 수식5.4.1(위 단락에도 수식 기술함) 과 같이 잔차의 절대값의 합에 대한 수식을 최소절대편차라고 한다. 교재에서는 최소제곱법 도출을 위한 과정처럼 설명이 되었으나, 실제로는 현대에도 활발하게 사용되는 방법론으로 보인다. 때문에 공부의 흔적을 남기기 위해 추가로 기술하였고, 좀 더 자세한 공부는 교재의 범위를 넘어서므로 차후의 일로 남겨둔다.
최소제곱법으로 선형회귀하기
최소제곱법을 통해 가중치(w)들을 구하는 방법은
- 각 w를 변수로 한 편미분(partial derivative)을 한 후,
- 각 도함수가 0이 되도록 놓음
- w의 갯수만큼 방정식이 나오므로 연립방정식(set of equations) 형태로 풀어서 w를 구함
- 도출한 w들이 바로 파라미터(parameters)
과정만 놓고보면 무척 간단하다. 그런데, 난 1과 2에서 한동안 막혔다. 왜 그렇게 하는지 도무지 알 수 없었기 때문이다. 위키 문서와 교재에서 모두 당연하다는 듯이 과정만 설명을 해 놓았으므로, 스스로 깨우치지 않으면 안되는 부분이라 생각하여 머리 나쁜 나는 한동안 무척 고심을 했다. 다행히도 오랜동안 생각을 하다보니 이유를 알 수 있게 되었다. 이유가 너무 간단해서 쪽팔리긴 하지만, 장고 끝에 얻은 내용을 따로 포스팅 하였다. (아래 링크 참고)
최소제곱법(least squares method)이 편미분을 하고 편도함수의 출력을 0으로 놓는 이유
교재 '인공지능을 위한 수학' 응용편의 최소제곱법에 대한 내용을 공부했었다. 아래는 이를 정리한 포스트다. 5장 선형회귀(4절:최소제곱법으로 파라미터 도출하기) - 응용편 - 인공지능을 위한
swjman.tistory.com
'Book Study > 인공지능을 위한 수학' 카테고리의 다른 글
| 5장 선형회귀(6절:완성된 모델 평가하기) - 응용편 - 인공지능을 위한 수학 (0) | 2021.02.26 |
|---|---|
| 5장 선형회귀(5절:정규화로 과학습 줄이기) - 응용편 - 인공지능을 위한 수학 (0) | 2021.02.22 |
| 5장 선형회귀(3절:선형회귀 모델) - 응용편 - 인공지능을 위한 수학 (0) | 2020.11.16 |
| 5장 선형회귀(2절:데이터 세트 'Boston Housing Dataset') - 응용편 - 인공지능을 위한 수학 (0) | 2020.11.16 |
| 5장 선형회귀(1절:회귀 모델로 주택 가격 추정하기) - 응용편 - 인공지능을 위한 수학 (0) | 2020.11.15 |
